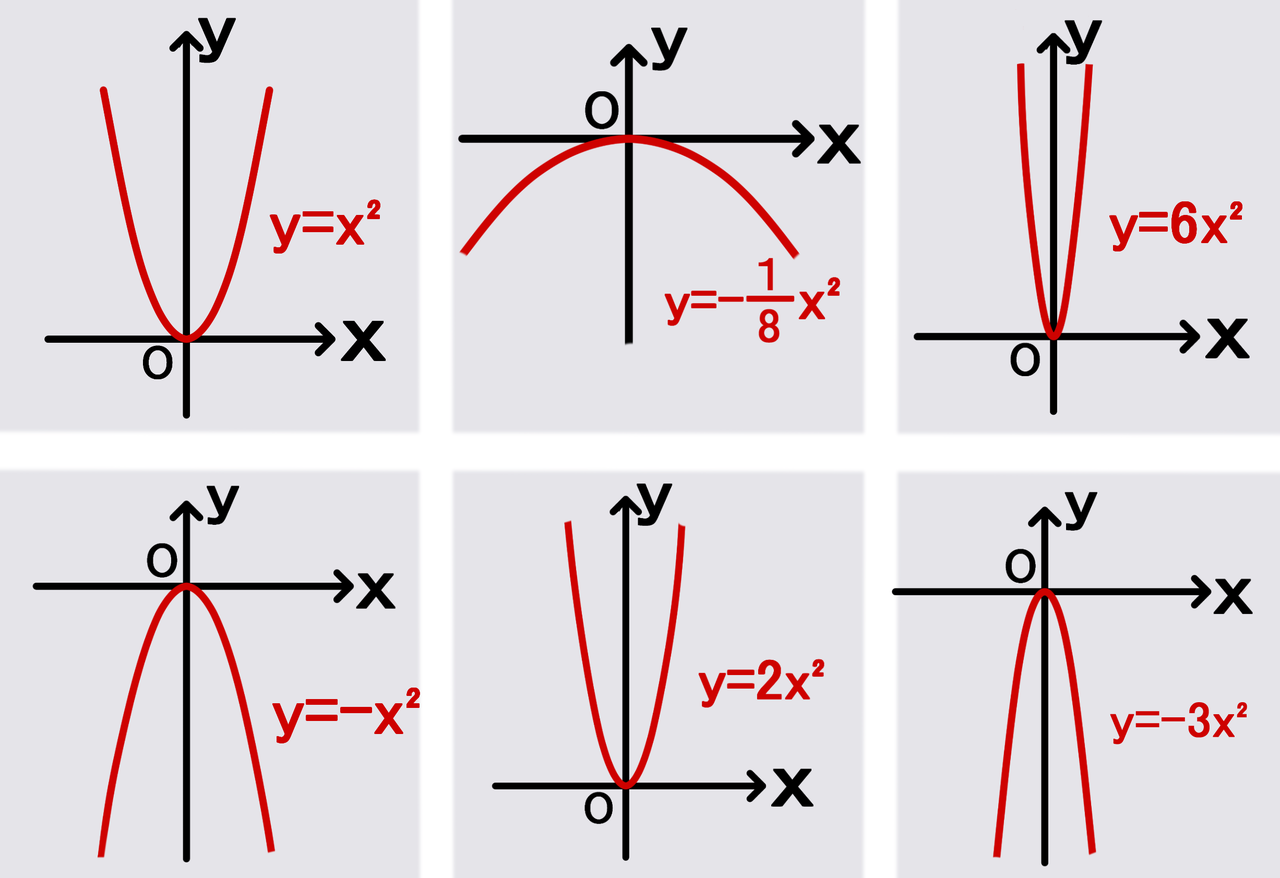
二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいく二乗に比例(ひれい)とは、y=ax 2 の式のように「yの値がxの2乗に比例する」ことです。aを比例定数(ひれいていすう)といいます。二乗に比例するグラフを下図に示します。 比例定数aが正、負のときでグラフの向きが変わる点に注意しましょう。またxにもう少し正確に説明しましょう。1変数の場合、例えばy= x2 x 2 1 2 のグラフはy= x2 のグ ラフにy= x 2 1 2 のグラフの高さを足したものですが、全体として下に凸の放物線であることに 変わりありませんでした(図6)。このことは、 x2 x 2 1 2 = (x 1 4)2 7 16
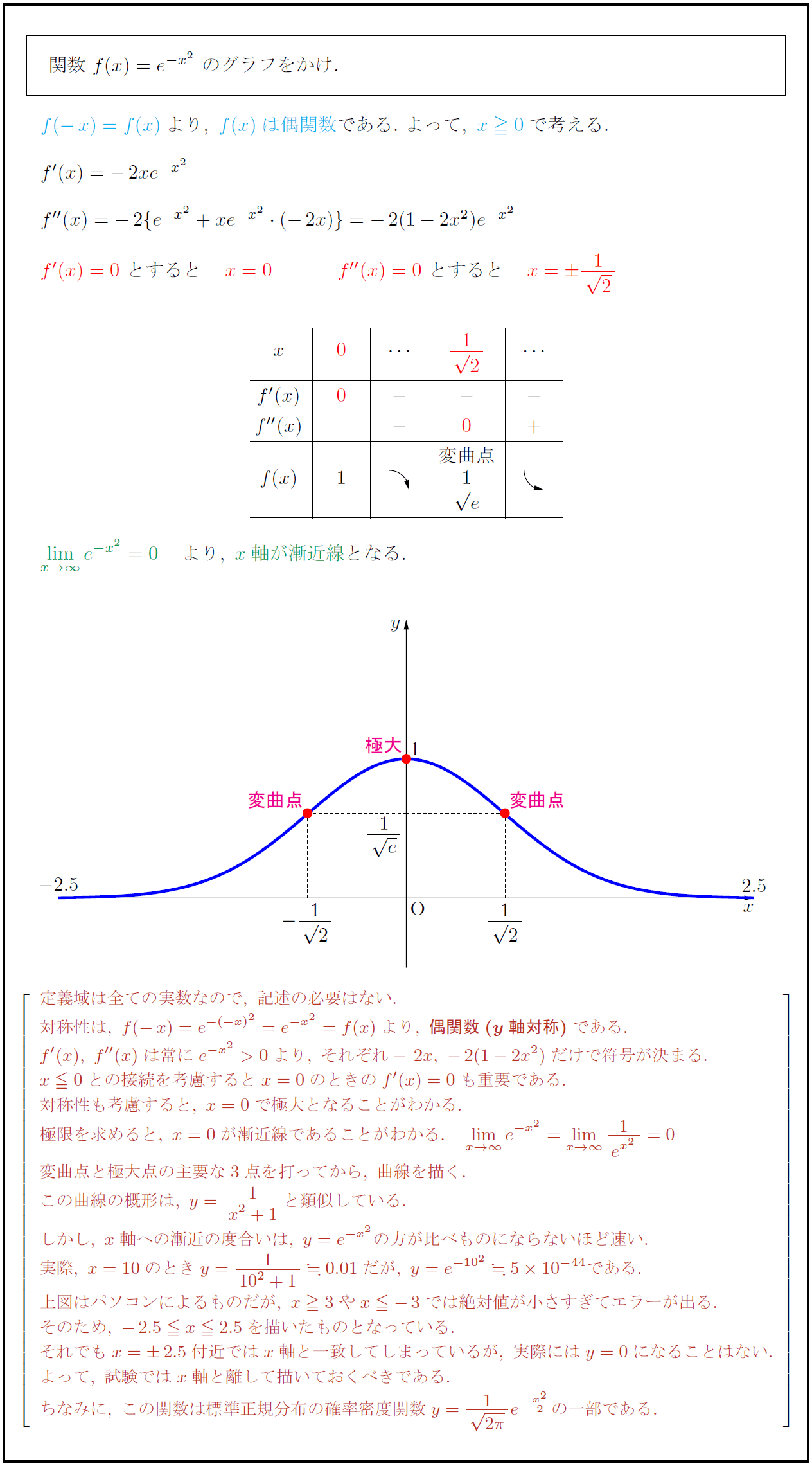
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月
Y=x2乗 2x グラフ
Y=x2乗 2x グラフ- y=3X2乗−12X−2 の解き方を教えてください。 昔に習ったんですけどやり方を忘れました 学校・仕事トーク 関連するQ&A 1 2次関数g=x二乗xのグラフとx軸の共有点の座標は、2次方程式x二乗x=0の解であるので、x=0 2 数学 二次関数のy= 3り二乗 4x 1のグラフとx軸の共有点の個数「 」である 二次あんころもち y=1/2x^2 (二分の一エックスの二乗)のグラフを書いてみたのですが、これでいいのでしょうか グラフに点を取るときに、偶数を当てはめたんですが (a=1/2のため)、そうすると点は2と4 (2と4)しかとれません xが4以上の時は大雑把にこれ




高校数学 無理関数 Y X 1 X のグラフ 斜め楕円 受験の月
最後に、一般の2次関数 \y=ax^2bxc\ のグラフについて考えてみよう。たとえば \y=2x^24x1\tag{1}\label{y=ax^2bxcnogurafu}\ のグラフを描くには、次のように式を変形(平方完成 (completing square) という)してから考える。 \begin{align} y=&2x^24x1\\ =&2\left\{x^22x\right\}1\\ &\quad\blacktriangleleft x^2の係数でくくる\(y=2x^2\) のグラフと同じ放物線になります。 そうなんです、「同じ」なんです。 曲線の曲がり具合とか、同じなんです。 ただし、 座標平面上のどこに曲線があるか、が異なります。 \(1\)次関数でも似たようなものでしたね。 \(y=2x\) と \(y=2x4\) は、Y = x 2という式をエクセルに渡しても理解しません 代わりに y = x 2という式を使った数値の表を作成して、それをグラフにします セル に 0 、セルB2 に=^2 と入力します。 キャレット ^は一般的な Windows キーボードの右上の方にあります、詳しくは →
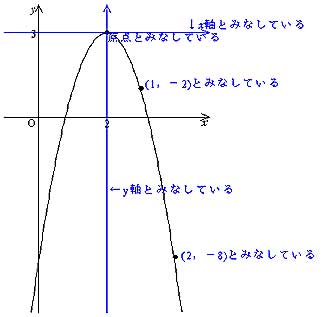
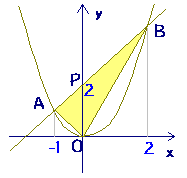
y=(x2) 216というグラフの頂点の座標は(2,16) したがって、 二次関数y=2x 2 8x10のグラフの頂点の座標は、(2,2 )となります。 二次関数グラフの書き方&頂点のまとめ 二次関数グラフに関する解説はこれで終わりです。 二次関数のグラフは、数学の分野の中でも非常に基礎的な事柄の1つ二次関数 y = x 2 − 3 x y=x^23x y = x 2 − 3 x 上の点 A (1, − 2) A(1,2) A (1, − 2) における接線の方程式を求めよ。 解答 y ′ = 2 x − 3 y'=2x3 y ′ = 2 x − 3 であり, x = 1 x=1 x = 1 における微分係数は − 11 − 1 である。 よって求める接線の方程式は, y − (− 2) = − 1 (x − 1) y(2)=1(x1) y問1 y=2x 2 のグラフ上に2点A,Bがあります.A,Bの x 座標がそれぞれ −1, 2 であるとき,次の問いに答えなさい. (1) 2点A,Bの座標を求めなさい. (2) 2点A,Bを通る直線の方程式を求めなさい. (3) 2点A,Bを通る直線が y 軸と交わる点Pの座標を求めなさい.
MathAquarium例題2 次関数 1 2次関数 1 2次関数のグラフ 次の2 次関数の頂点と軸を求めよ。また,(1)はグラフもかけ。 (1) y=-x2+2x+1 (2) y=x2+ax-a y=ax2+bx+c の形からy=a(x-p)2+q の形に変形することを「平方完成」といいます。 高校数学で頻繁に出てくる重要な変4 関数y=ax2 のグラフと変域(1) VMA05 3 2 乗に比例する関数の増加・減少 ここでは,関数y=ax2 の値の増加・減少について学習してみましょう。 関数y=ax2 でxの変域が与えられたときのyの最大値・最小値は,たとえばa>0 のとき のように, xの変域によって考え方が違ってきます。関数\(y=x^22x3\)上の点\((2,3)\)における接線の方程式を求めよ。 それでは、接線の方程式を求める手順を確認しましょう。 まずは、 関数の式を微分して、接点の\(x\)座標を代入。



二次関数のグラフ




解説がわかりません なぜy x2乗 3xを平行移動した放物線の二次関数はy x2乗 Clear
おわりに ここでは、二次関数 y = ax2 q y = a x 2 q のグラフについて見てきました。 このグラフのかき方は、次のようになります。 頂点 (0,q) ( 0, q) を把握し、座標を書く 頂点をもとに、放物線をかく 放物線上のどこか1点の座標を書く 放物線上のどこかMathway 代数問題ソルバー Mathway ウェブでMathwayを訪問する Google Play で無料ダウンロード iTunes で無料ダウンロード Amazonで無料ダウンロード Windows ストアで無料ダウンロードY = x x のグラフ 微分が分かったので、グラフを書いてみましょう。 x = − 1 のとき、つまり、 x = 1 e のときです。 となります。 よって、グラフは図のようになります(定義域は x > 0 です)。 極小値(かつ最小値)は、 ( 1 e) 1 e ≒ 069 です。 である



授業実践記録




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
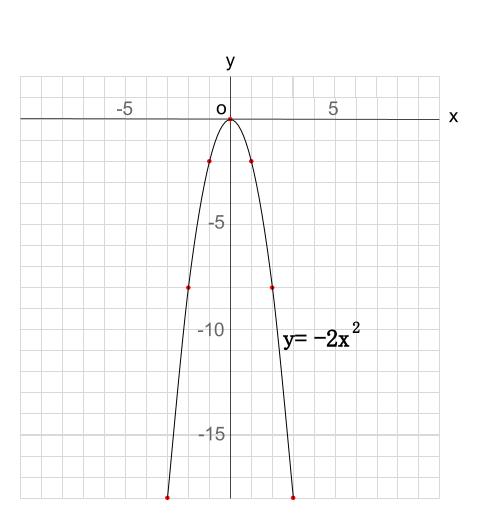
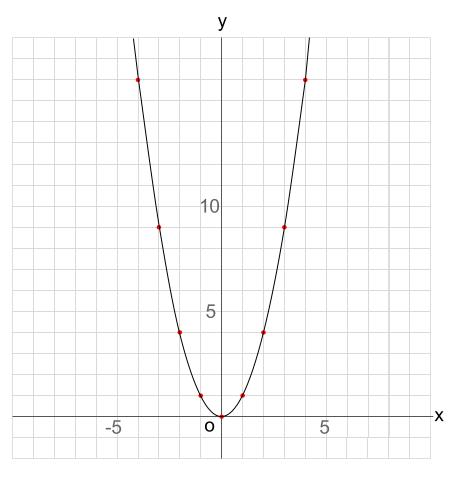
仮に x = 2 の時を調べてみましょう。 この時のグラフの傾きは、y'の式に代入すると15となります。この時のy'の符号が重要となります。 x = 2 の時、y'の符号が正であるためこの区間ではグラフの傾きが正 = グラフが右上がりであることがわかります。 y=x 2 上の点(10 , 100) 問題① まず、yを微分しましょう。 y´=2x となりますね。 すると、求めたい接線の傾きは、y´=2xにx=10を代入すればよいのでした。 したがって、(求めたい接線の傾き)=2・10= となります。 求めたい接線は(10 , 100)を通るのは問題文から分かっています。 なので、傾きがでY=x 2 のグラフ と同じように、式を満たすxとyの値の組 を座標にとっていくと、点が隙間なくうまって下のよう な滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック! y=2x 2 のグラフの特徴 y軸に対して対称 下に凸 x>0の範囲でyは増加 x<0の範囲でyは減少 x=0の時、y=0 この




例題で学ぶ高校数学 Y Ax2 Q



Q Tbn And9gcr5xwf9edrcskejqgyagxfwhnmwvaa7xrvtcx Jl9p Kp5wcn6m Usqp Cau
「実数yの立方根」、「実数yの三乗 根 (∞,∞)で定義された1変数関数y=f (x)= x 3 の逆関数のグラフ ・「(-∞,∞) で定義された1変数関数 y=f (x)= x 3 」のグラフを、 通常とは逆に、 「yの値を一つ決めて、それに対応するxの値(yの値の逆像)を読み取る」 という方向で読み取ると(→右図・y=ax 2 q のグラフ ↓ →例題 ↓ y=ax 2 q のグラフ y=ax 2 q のグラフを y=ax 2 のグラフと比較しながら考えてみます。 やはり表を作ってみることが大切です。 下の表は 2x 2 と 2x 2 1 を比較したものです。 xのどの値においても, 2x 2 1 の値は 2x 2 の値に1を足したものです。 したがって, y=2xY=x 2 のグラフをx軸方向に+1平行移動したグラフで、頂点は(1,0)となることがわかります。 では、次の式ではどうでしょうか。 y=x 2 -2x




Y 1 2x 2 二分の一エックスの二乗 のグラフを書いてみたのですが これでいいの Clear




Y 3分の1x2乗 2xのグラフの x切片の求め方を教えて下さい Y 0のときの途中 Clear
グラフが放物線 \(y = x^2 2x 4\) を平行移動したもので、点 \((0, 3)\) と点 \((−1, 10)\) の \(2\) 点を通る放物線の方程式を求めよ。 また、\(x\) 軸、\(y\) 軸方向にどれだけ平行移動したグラフか。 求める式を \(y = ax^2 bx c\) とおき、通る \(2\) 点をそれぞれ代入すれば \(b\)、\(c\) の値が出てきます頻出問題 代数 グラフ y=1/2x^2 y = 1 2 x2 y = 1 2 x 2 1 2 1 2 と x2 x 2 を組み合わせます。 y = x2 2 y = x 2 2 与えられた放物線の性質を求めましょう。 タップしてもっと手順を表示する Rewrite the equation in vertex form例題3 y=2x 2 のグラフ を x 放物線 y=2(x2) 2 1 をよく見て見ますと,この式の中に頂点 (2,1) の座標が表れています。 上の結果を,実際,右のグラフをマウスを用いて確かめてみましょう。 一般に,次のことが言えます。 まとめ2 (放物線の頂点と軸) y=ax 2 のグラフを,x 軸方向へ p,y 軸方向へ
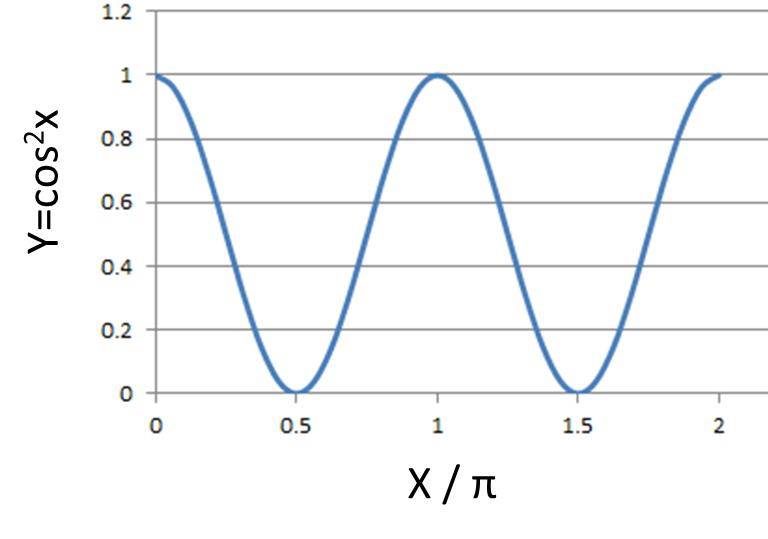



Y Cos 2x のグラフや周期は Y Cos 2 8を微分するとどうなるのか ウルトラフリーダム



2次関数y X2乗 2x 2 X 1 のグラフ 最大値 最小値 Yahoo 知恵袋
y=2x二乗+x−1をX軸方向に1,Y軸方向に−2だけ平行移動したグラフの方程式とY軸対称 、原点対称のグラフの方程式を解いてください。お願いします。 高校数学 aの二乗2a−1=0を解いてa=−1±√2とするやり方が分かりません!教えてください 数学 数学の問題教えてください! 2次関数Graph the parabola, y =x^21 by finding the turning point and using a table to find values for x and y例:y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



二次関数の移動
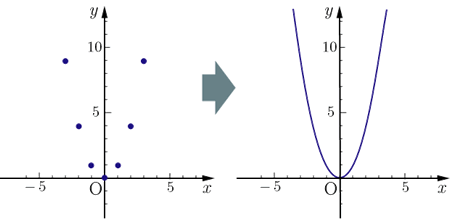
中3数学。2乗に比例する関数 (y = ax²)。この a は「変化の割合」? xの値が「0から2まで」増加する? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツ、成績アップ法を公開。X 2 2次関数の最も簡単な関数は y =x2 y = x 2 である.この関数についてグラフを考える. x x の値3,2,1,0,1,2,3に対する y y の値をを下の表に示す. 各 x x , y y の組に対応する点を座標平面に描くと左下の図のようになる.表のような y = x2 y = x 2 の例題5 2次関数 y=x 2 2x の頂点,軸を求め,グラフを書け。 解答まず,前回の章で練習したように,与式を標準形に直します。 y=x 2 2x=(x 22x)={(x1) 21} ∴ y=(x1) 2 1 となりますので,頂点は (1,1),軸の方程式 x=1 となります。このことを用いてグラフを描くと,右図のようになります。 グラフ




2次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア




y x2乗 2x 8の頂点はいくつですか Clear
y = a x y 2 = a x y=\sqrt{ax}\iff y^2=ax y = a x y 2 = a x かつ y ≥ 0 y\geq 0 y ≥ 0 なので,グラフは放物線の一部になります(よく見る y = x 2 y=x^2 y = x 2 という放物線を 9 0 ∘ 90^{\circ} 9 0 ∘ 回転させたものの半分)。 b ≠ 0 b\neq 0 b = 0 の場合は平行移動すればよいだけです。Y = x 2 上の点 (1, 1) における接線の方程式 y'= 2x だから x = 1 のとき y'= 2 y−1 = 2(x−1) y = 2x−1 ・・・答 y = x 2 上の点 (1, 1) における法線の方程式 法線の傾きは m'=− y−1 =− (x−1) y =− x ・・・答 (2) y = x 2 −2x における傾き −4 の接線の方程式 考え方 : f'(a) → a → f(a) の順に求めます。 y #!/usr/bin/python3 # coding UTF8 #グラフ y=sqrt(r^2x^2) import matplotlibpyplot as plt import numpy as np r = 10 x = np linspace (r, r, , endpoint = True) y = np sqrt (r ** 2x ** 2) plt plot (x, y, 'red') #実線 plt plot (x,y, 'red') plt axes () set_aspect ('equal', 'datalim') #xとy軸を同じ比率にする plt xticks (rotation = 45) # x 軸のラベルの文字が



2乗に比例するグラフ 中学から数学だいすき




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks
Y=ax2乗のグラフ書き方 まとめ お疲れ様でした! 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ! これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ! 練習 (/・ω・)/第4章 基本的な関数の計算とグラフ 対数関数 対数関数 y=f(x)=log a x は 指数関数 y=g(x)=a x の逆関数。 対数値の意味:数a(底)をx乗するといくらになるか? 答はa x である。 これは指数関数の発想である。対数値は、数aを何(y)乗すると数xになるだろうか?Y=x2乗-2x-2を平方完成したらどうなりますか? 途中式教えてください 0 回答 いちご姫🍓 2年以上前 こんな感じです! 0 この回答にコメントする この質問に回答する 似た質問 高校生 数学 (3)です。 赤い文字が答えになります 解説をお願いしたいです🙇♀️ 高校生 数学 68が




例題で学ぶ高校数学 Y A X P 2




高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月
まずは、簡単でいいので\(y=2x^2\)のグラフを書き、それを\(2≦x≦4\)で切り取ってみましょう。 すると、赤く塗った部分が切り取られることになります。 このとき、タテの範囲はどうなっているかというと このように、\(x=4\)の部分である\(y=32\)が一番大きく、\(x=2\)の部分である\(y=8\)が一番文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R=(-∞,∞) で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。




数学 中3 35 二次関数のグラフ Youtube




基本 二次関数y A X P 2のグラフ なかけんの数学ノート
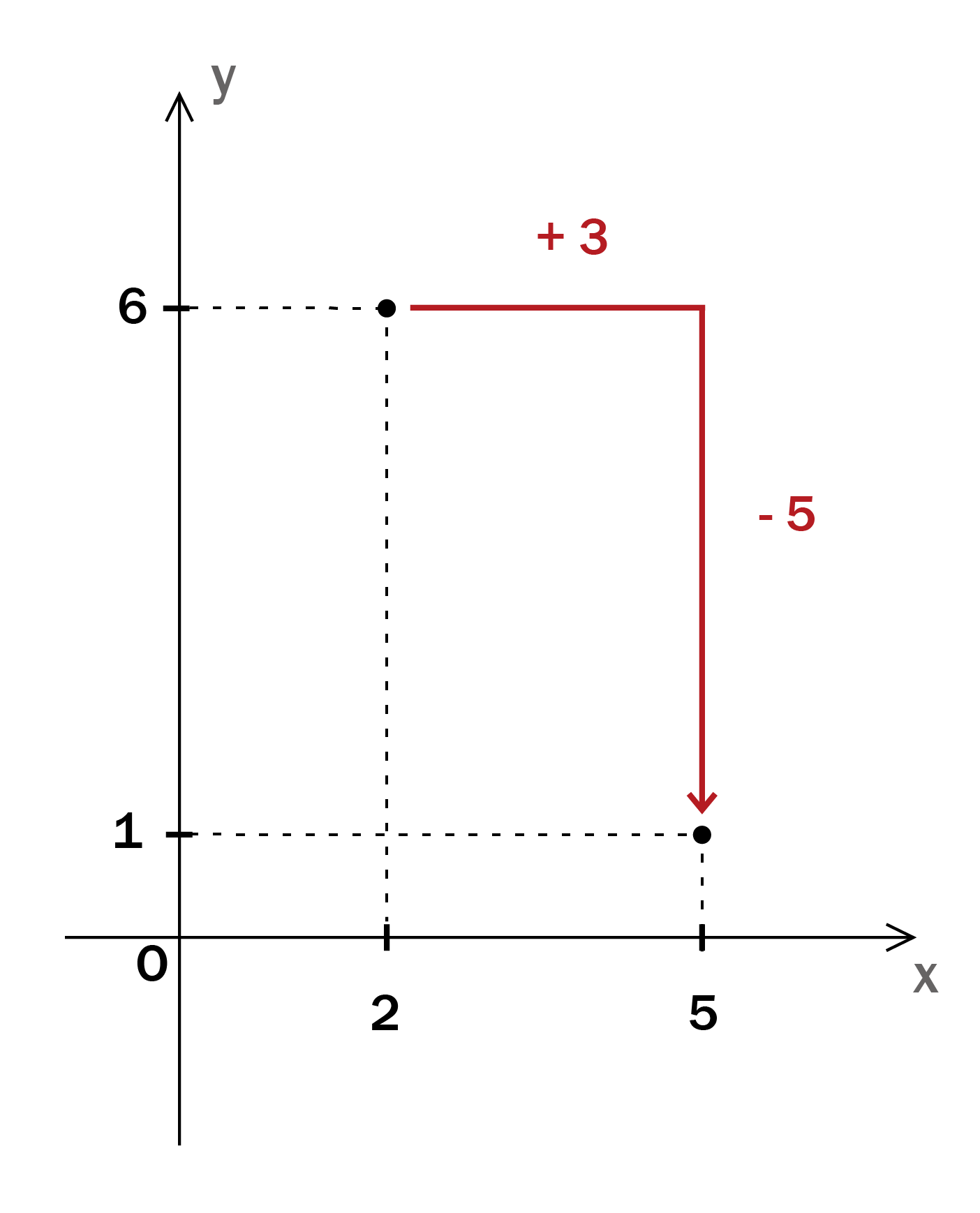



二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



二次関数のグラフ



グラフを教えてください y x二乗 2x 3 のグラフ Yahoo 知恵袋




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks




高校数学 無理関数 Y X 1 X のグラフ 斜め楕円 受験の月



2乗に比例するグラフ 中学から数学だいすき




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学



1




Aは正の定数とする 関数y X 2 4x 3 0 X A の最大値を求めよ 解き 高校 教えて Goo



2 裏業




3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



Y 3分の1xの2乗の関数のグラフはどのようにしてかけばいいの Yahoo 知恵袋




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




番で X二乗 2xを置き換えるというのは分かるんですけど その先がどうすればいいか Clear



2次関数のグラフと直線




Aは正の定数とする Clear



Y X2乗 2x 3ってどうしてこの様なグラフになるのでしょうか Yahoo 知恵袋




基本 無理関数のグラフ 放物線の一部 なかけんの数学ノート




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



1 の問題で関数y X2乗 1を平方完成をしないのは二次関数と書いてな Yahoo 知恵袋



2次関数のグラフ Y X 2



図のように関数y X2乗とy Ax Bのグラフが 2点a Bで交わ Yahoo 知恵袋



2次関数のグラフの問題です 放物線y x2乗と直線y Ax Bは2点a bで Yahoo 知恵袋
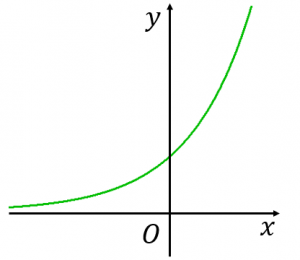



Y E Xのグラフをきれいに書く6つのコツ 具体例で学ぶ数学




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



授業実践記録



Y X2乗 2 X のグラフの式を教えてください 2乗は 2 Yahoo 知恵袋



1




2次関数のグラフ 2次関数のグラフの式の 頂点の求め方を教えて下さい Okwave



授業実践記録




Y 1 X 2乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo



二次関数のグラフ 二次不等式 戻る 頂点が原点 0 0 の二次関数グラフは中学3年で学習しました 思い出してください下のグラフは2次関数 つまり は の2乗に比例するグラフ Y Ax2で表します 仮に比例定数 2として Y 2x2のグラフを書いてみま




Y 1 X2乗のグラフ Youtube



指数方程式
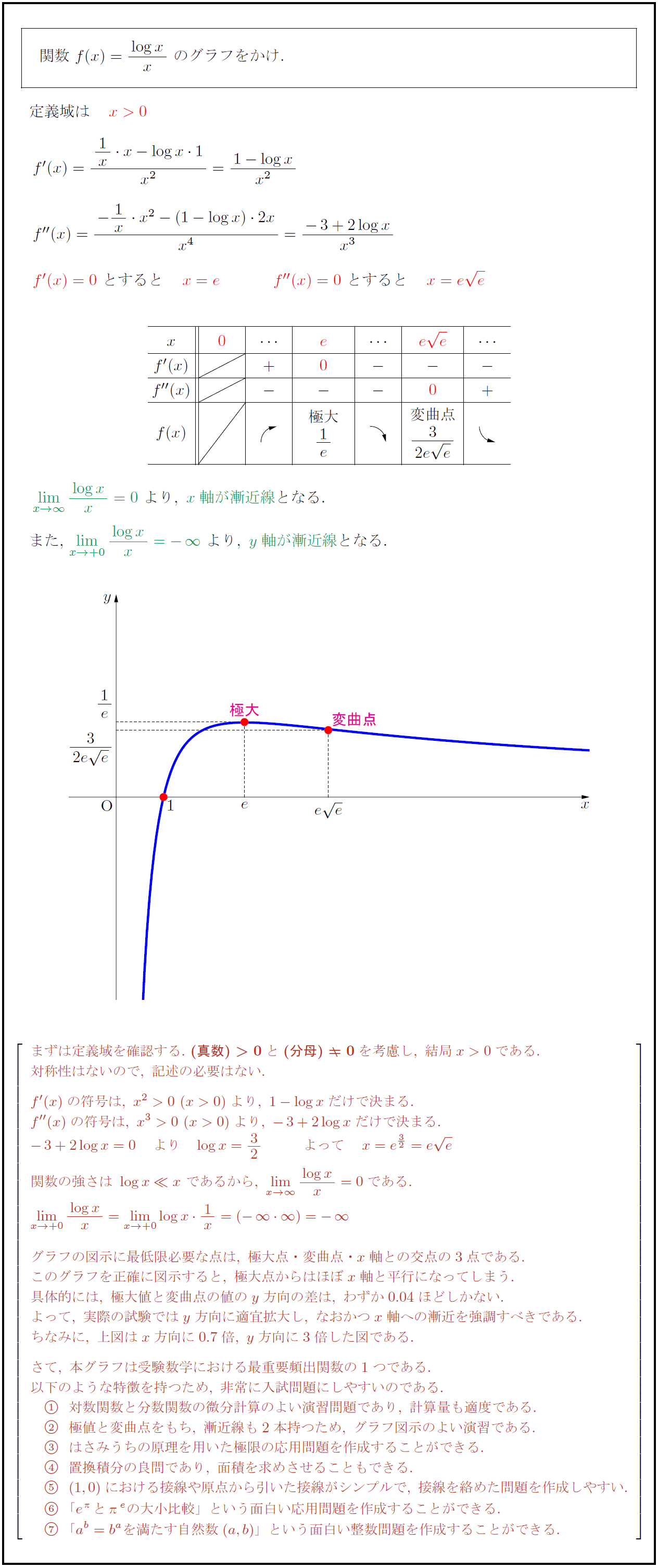



高校数学 対数関数 Y Logx X のグラフ 受験の月




中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




2次関数のグラフと直線



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋



2次関数y X2乗 2x 3 2 X 2 の最大値 最小値の問題 最 Yahoo 知恵袋



Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋
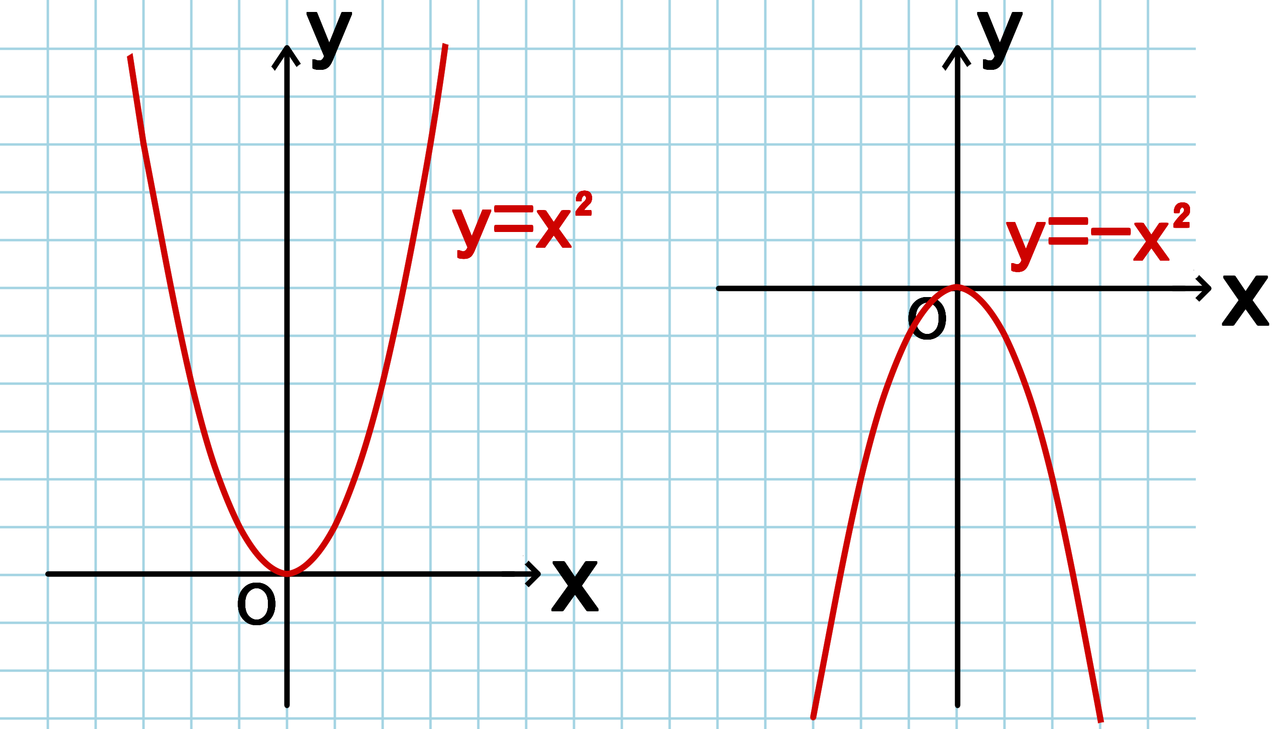



2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学



Y x2乗 4x 4のグラフってどうなりますか 頂点と軸と凸 Yahoo 知恵袋




中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube




基本 指数関数のグラフ なかけんの数学ノート




2次関数のグラフ



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ
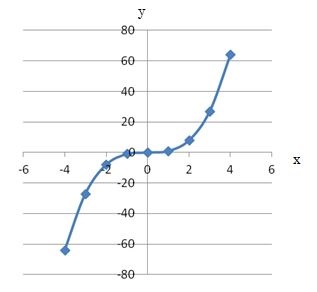



3次関数 方程式 のグラフ もう一度やり直しの算数 数学



二次関数の質問です 写真の問題の解き方を教えてください 答え A Y Yahoo 知恵袋



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su




例題で学ぶ高校数学 Y Ax2 Q



1



Y X2乗 2 X のグラフの式を教えてください 2乗は 2 Yahoo 知恵袋



数学で 右の図のように 関数y x2乗のグラフ上にx座標が Yahoo 知恵袋




例題で学ぶ高校数学 Y A X P 2




Y X 2 2x 3の平方完成について X 2 2x 3 X 1 2 4 となったので 数学 教えて Goo



Y 2分の1x2乗のグラフ y 4分の1x2乗のグラフの書き方を教えて Yahoo 知恵袋



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師




この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave



中3 2次関数




数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo



中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su




中3数学 Y X2乗のグラフ 5分で学習 Youtube



因数分解とグラフ 中学から数学だいすき




4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo
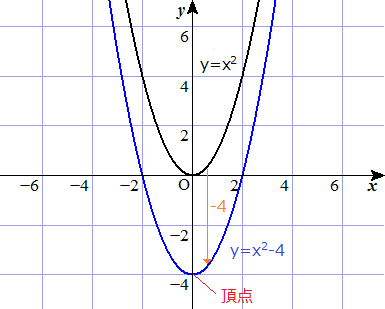



例題で学ぶ高校数学 Y Ax2 Q




y x2乗 2x 2を平方完成したらどうなりますか 途中式教えてください Clear



Y 1 X2乗のグラフ Youtube



Y X2乗 4x 1のグラフの軸と頂点の求め方を教えてください お願いし Yahoo 知恵袋



Yx2乗 ニスヌーピー 壁紙
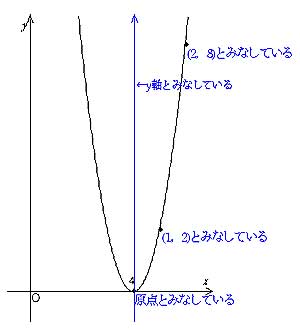



授業実践記録
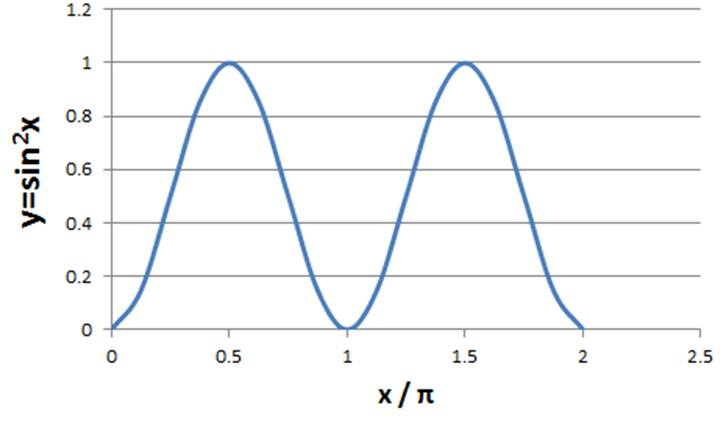



Y Sin 2x のグラフや周期は Y Sin 2 8を微分するとどうなるのか ウルトラフリーダム
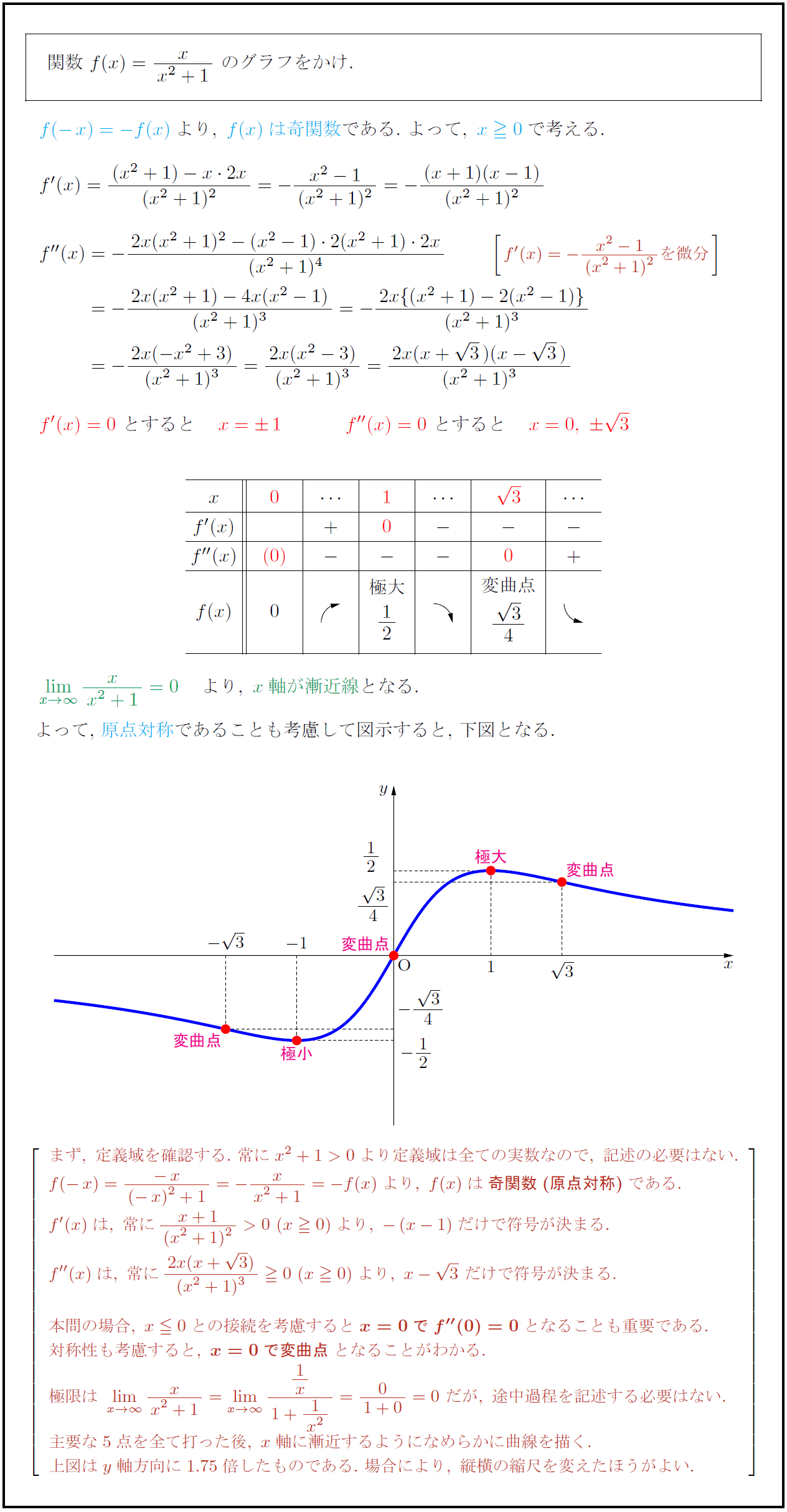



高校数学 分数関数 Y X X 1 のグラフ 受験の月




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




ガウス記号 2 Y X 2 のグラフを書こう 身勝手な主張




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




Aを実数の定数とする 二次関数y X 2 2ax A 2 1の0 X 2における最小値 高校 教えて Goo
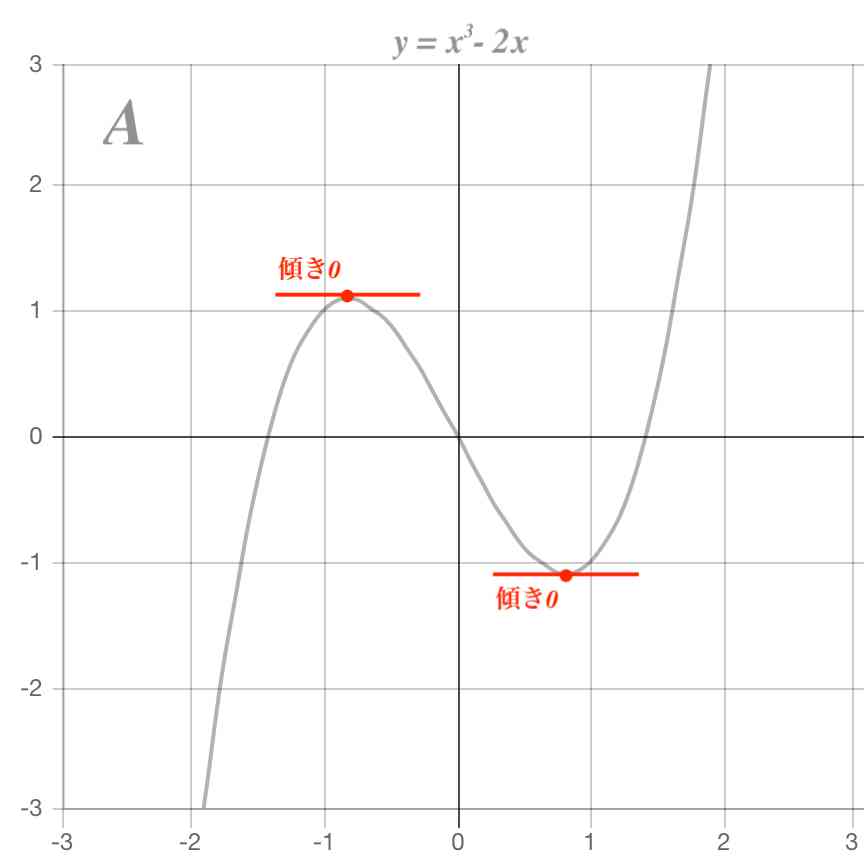



三次関数のグラフの書き方



Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋
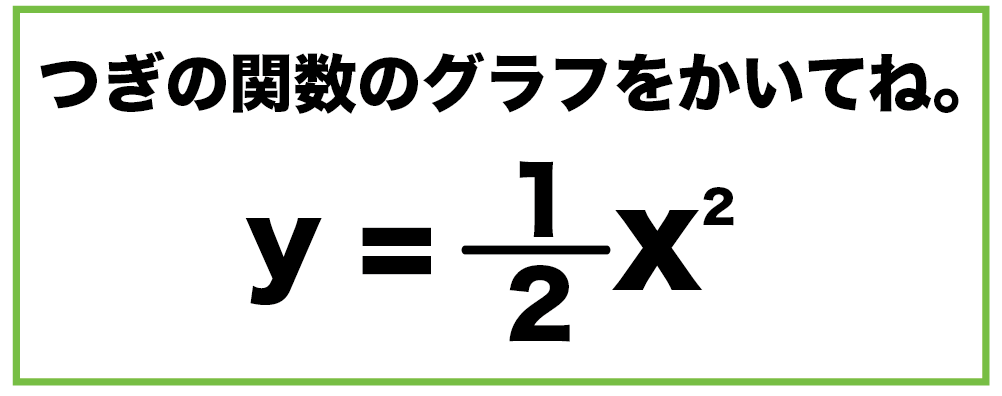



中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



0 件のコメント:
コメントを投稿